日常生活中,當我們步入音樂廳、演播劇院、教室或教堂,甚至於一個大空間的辦公場所,往往會下意識的覺察到所感受的“音質總題”,但是只有少數的人能夠解釋“良好的音質和不好的音質”的真正的意義,了解影響或產生某些聲學特性的因素,至於知道室內音樂是受一些能夠按科學方法加以處理的原理所支配的人就更少了,本章試圖通過室內聲學和擴聲的基本原理的討論,使讀者對室內聲學做到“如其然全知其所以然”,並在實際工作中掌握運用。
2.1室內聲學特徵
聲學的基本理論告訴我們,空氣中的某一點產生振動時,即引起該聲源周圍的一系列的聲波,它們的波振面沉着半徑逐漸增加的同心球面層層向外傳播。隨着現聲源的距離增大,各點聲強逐漸減弱,如果沒有遇到任何障礙物,則聲音減弱到直到聽不見,但是在室內容發音時,聲音的傳播受到封閉界面的限制,其聲音在各個界面來回反射,出現了許多複雜的干涉現象,情況與在自由空間時很不相同。那麼它們的聲場情況到底是怎麼樣呢?下面我們就是實用性較強的,亦是通常運用於音質設計中對室內聲場分析的基本方法來分析和敘述,在必要時以適當的波動聲學的論點加以說明。
2.1.1聲場分析
1)幾何聲學方法
我們把聲波的傳播途徑用聲線繪出,可以找也直達聲和頭幾次反射聲所可能出現的分佈情況,或從改變界面的形狀以控制這些反射聲,這就是我們常稱的幾何圖解法,它和幾何光學的假設相類似,見圖2-1,即入射聲線與反射聲線出現在同一平面內,入射角等於么射角。
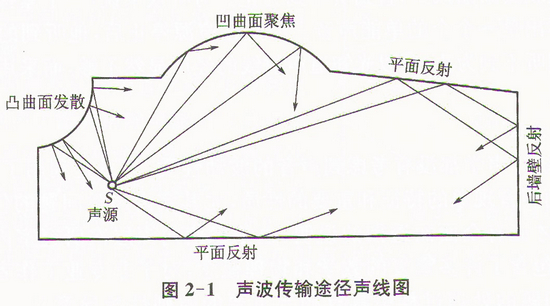
幾何聲學只有在聲波的波長雙反射面尺寸小得多時才正確,但它可以使我們從房間的縱、剖面來了解聲波在室內經過若干時間以後的反射情況,當然聲波在壁面上反射多次以後,反射聲線就已相當複雜的紊亂,甚至接近無規則分佈了。
2)統計聲學方法
當聲源S在室內開始發聲時,亦即當開始輻射聲能時,這些形成的聲波首先在室內自由傳播,見圖2—2。
經過一段時間t后,首先有一直達聲波O到達P點,P點的聲強大小隨SP的距離增大而減弱,時間t由SP的距離決定。在若干時間以後,又有由不同壁面反射來的聲波1、2、3、……到達P點,它們的強度分別由不同壁面的吸收條件與SAP、SBP、SCP等的距離來決定,時間t1、t2、t3等則分為各反射聲,到達P點所需的時間。如聲源恆穩地繼續發聲,則各自反射波與入射波相繼疊加加起來,見圖2-3。這種現象一直一直持續到一定時間tn以後。P點的聲強即逐漸到達恆穩狀態,第n次反射到P點的聲強已經很少而可以忽略不計了,於是室內聲音能不再增強,此時界面在每一個單位時間吸收了和聲源輻射相等的聲能。
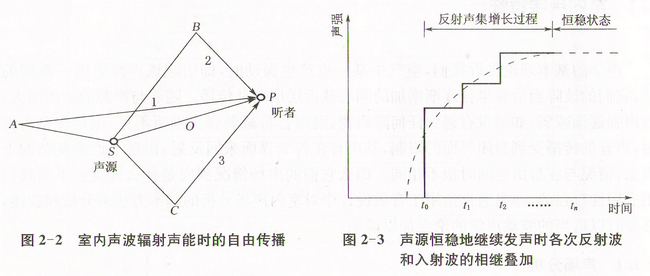
如室內表面的吸聲效果差,則聲音每次反射所損失的能量都很有限,反射波所集起的總聲強就要比直達聲波自己的強度高多了,只要聲源繼續發音,該年總是保持這樣高的強度,這一現象使我們更清楚的了解到某一刻聲源停止時,反射波並不能同時消失,而要繼續在室內回傳播一段時間,以後每次受到反射時,每一個聲波都因為吸收而失去一部分的能量,室內的總聲能就要漸漸減少,直到聽不到為止。對聽眾來說,一個緊接一個的聲波射入耳中,使它分辯不出是一個個的單能聲音。因此在聲源停止后,他聽到的好像是聲音仍在延繼,漸漸變弱直到聽不到為止,所以光知道聲射線的經歷顯然不夠,而採用統計方法可以了解聲射線的總體。
3)波聲學方法
幾何聲學和統計聲學都沒有考慮到聲音的波動性,而只是利用了聲射線與反射的純幾何圖,然而聲音現象和特徵和重要的性質,尤其室內聲學問題的仔細考慮,只有在波動理論的基礎上才能有全面而透徹的說明,也是我們向深層次研究室內聲學的需求,問題是波動聲學卻包含了放許多繁複的數學物理概念,對於非專業工作者來說,並不是很熟悉,但在實際問題的處理過程中具有相當重要的原則性指導意義。本節略加敘述和介紹。
現在我們重溫一下幾何聲學和統計聲學應用到室內聲學情況。一般包含有下列幾個假設:①從聲源發出的射線經過許多次連續反射以後即處於完全擴散狀態;②在聲音的增強和衰減過程中僅考慮只有聲源頻率存在。但從實驗中我們知道,聲音在室內的增強與衰減除聲源頻率外,還有一些其它的頻率存在,這些頻率就是房間共振頻率,這些被激發的固有頻率的迭加,必然引起聲壓有起伏很大的漲落,聽音條件就有很大的不均勻性,而這些共振頻率的分佈均勻與否與房間的尺度、比例和形狀有着直接的關係:
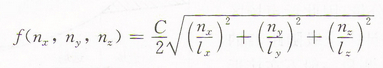
式中:f——各種可能的固有頻率;
Lx、ly、lz——房間的集合尺度;
C——聲音在空氣中傳播的速度;
Nx、ny、nz——可分別選擇從0→∞之間任何整數值。
從上式可以看出,波動聲學使我們更清楚的了解房間內的簡正振動方式,選擇合適的房間尺度、比例和形狀,可以減少或避免簡正振動方式的簡併,使本徵頻率分佈圴勻。
從上式還可以看出,房間的長(lx)寬(ly)高(lz)三者比例若成整數倍,簡正振動方式簡併,本徵頻率分佈不均勻,聲學響應變得很不規則;聲音在各頻率的衰減有明顯的差別,在小房間和低頻段尤為如此。所以我們在設計要求頻率範圍非常寬的播音室、錄音室等用房時,波動聲學的分析是很重要的。從分析中我們得出了房間三向尺度比例為2.4:1.5:1.0和3.2:1.3:1.0之間。
總之,實際工作中以統計聲學分析為主,以幾何聲學分析為輔,在吸收波動聲學中的一些有益的理論做為指導。
2.1.2 直達聲和么射聲
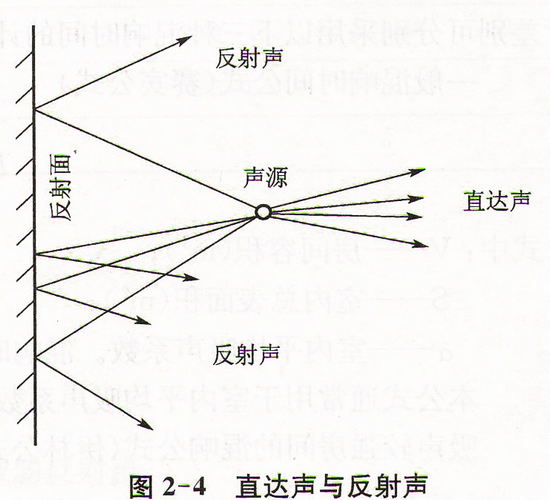
自聲源未經反射直接傳到接受點的聲音啊做直達聲;聲源經過壁面一次或多次反射到達聽者的聲音叫反射聲,見圖2-4而到達聽者耳朵的最鄰近牆壁的么射聲稱為近次反射聲。近次反射對直達聲起到加強加厚的效果。
在音質設計中,關於大廳形體方面的主要涉及直達聲、前次反射聲的控制和利用、聲擴散和防止音質缺陷等方面的問題。
我們的設計原則是充分利用直達聲,爭取和控制前次反射聲,加強聲擴散和消除的可能出現的聲學缺陷等幾個方面。具體的方法和途徑是:①縮短直達聲的傳播距離,避免直達聲被遮擋和被聽眾掠射吸收,恰當的利用聲源的指向性能;②調節反射面的傾斜角度,使反射聲(主要是反次射聲或稱一次反射聲)均勻分佈在整個聽眾席上;③增加擴散反射。
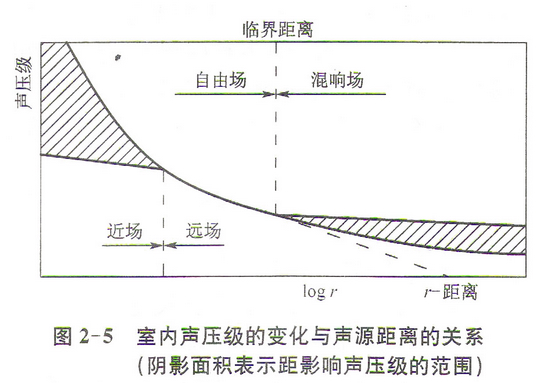
2.1.3近聲場和遠聲場
我們知道,室內總聲場是由直達聲場的反射聲場疊加而成的,但總聲場內聲壓級有個隨距離聲源點的區域變化關係,即近聲場、遠聲場。在近聲場,聲壓級現距離沒有簡單的關係,因為在該區域內質點速度與聲波傳播方向不一致,而是任意各點上都存在着明顯的切向速度分量,因此近聲場區不能按通常規律來估計聲壓級隨距離的變化,這也就是為什麼測量一般不在接近聲源尺度的二倍之內進行的原因。在遠的自由場地,聲級變化服從反平方定律。在遠的混響聲(式擴散場)聲能密度非常接近一致,見圖2-5。
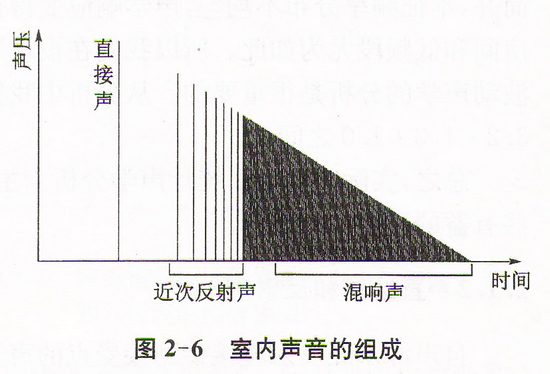
2.1.4混響和混響時間
混音:指聲源停止發聲衙,聲音由於房間中界面的多次反射或散射逐漸衰減的現象。根據以上所述,室內聲音主要由三部分組成,見圖2-6。
混響時間:指在室內聲音已達到穩定狀態后聲源停止發聲,平均聲能密度自原始值衰減到其百分之一所需要的時間,即聲源停止在發聲后衰減60dB所需要的時間。混音時間是目前音質設計中能定量估算的重要評論指標,這直接影響廳堂音質的效果。
目前的工程設計中,根據室內吸聲特性的差別可分別採用以下三種混響時間的計算公試:
一般混響時間公式(賽賓公式)
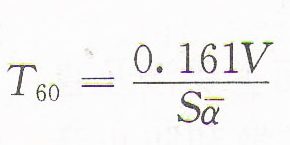
式中:V——房間容積(m3);
S——室內總表面積(m3);
ā——室內平均吸聲係數。混響時間T60的單位是秒(s)。
本公式通常用於室內平均吸聲係數小於0.2的情況,否則將產生較大誤差。
吸聲較強房間混響公式(伊林公式)
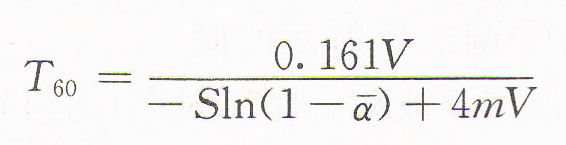
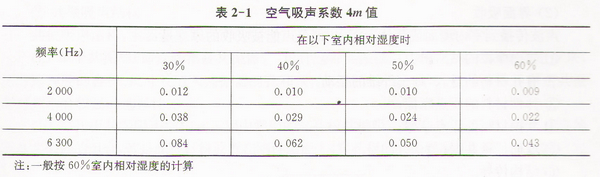
式中:m——空氣吸聲係數(室內溫度20℃時,4m值見表2-1)。
室內三對錶面吸聲不同時的混響公式(肥茨羅伊公式)
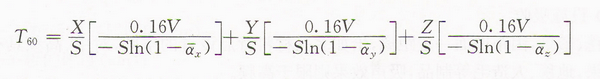
式中:X、Y、Z——相應三對內表面面積(m2);
āx、āy、āz——相應X、Y、Z三對錶面的平均吸聲係數;
V——房間容積(m3);
S——室內總表面積(m2)。
該式適用於室內三對錶面上吸聲分佈不均勻的場合。
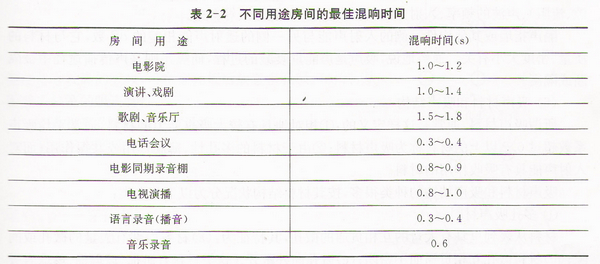
常用廳堂最佳混響時間(500Hz)如表2-2。



-1024x683.jpg)